Here is the problem
"lets set the internal resistance, ri, of the battery with emf Ei. equal to bEi where b is a constant assumed the same for all three batteries.
E1=5v
E2=10v
E3=15v
r1=bE1
r2=bE2
r3=bE3 http://i17.photobucket.com/albums/b51/chs2004/physics1.jpg
http://i17.photobucket.com/albums/b51/chs2004/physics1.jpg2.To decrease internal resistance we can connect the batteries in parallel, although this advantage could be offest by a decrease in net voltage. To test this hypothesis find the current flowing through the 200 ohm resistor, assume 'b' is the same from part one.
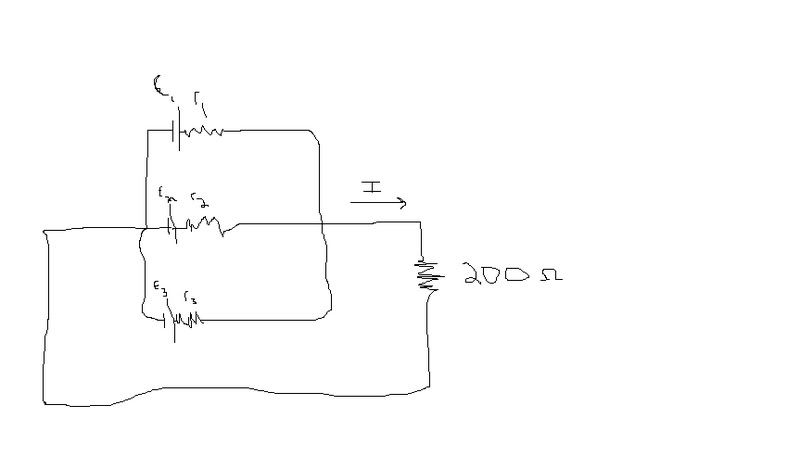 http://i17.photobucket.com/albums/b51/chs2004/physics2.jpg
http://i17.photobucket.com/albums/b51/chs2004/physics2.jpg2. Relevant equations
Kirchoffs's (sp) Loop Rule
3. The attempt at a solution
Ok - For part one i set up the loop rule equation as follows:
E1-(Ir1)+E2-(Ir2)+E3-(Ir3)-I(200ohms)=0After substituting in the EMFs and resistances i got the equation:
-2.6= -.137bE1 - .137bE2 - .137bE3From there i factored out the .137 and brought that to the other side and then factored out the 'b' and got:
19=b(5+10+30)
b=.6Im not sure i did that first part right, becuase for the second part when i figure out all the currents, I1, I2, I3, they all come out to the same thing becuase the equation, I=E/R, and R=bE, the EMFs just cancel giving me 1/b for each current, 1.7A=I1=I2=I3.
Then using I=5.1A solving for the deltaV across the 200ohm resistor i get:
DeltaV=(5.1A)(200ohms)=1020V (WAYYY too high)
Im not sure where im going wrong here...i tried this and another way and i still get a deltaV higher than the combined voltages of the three batteries
----the other way i tried the problem was like this:
using the equation: E=IR
I took the EMF of the first battery, 5v, and set the equation as follows:
5V=(.137A)(r1) ==> where r1=bE1
5V=(.137A)(5V)(B)
b=7.3
Using that value in the second part of the problem still gives me a voltage drop of 82V across that 200ohm resistor, which cant be correct.