HA
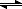
H
+ + A
-At equilibrium CA0-x x x
H2O
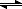
H
+ + OH
-At equilibrium something y y
[tex]
K_w=[H^+][OH^-] \\
K_w=(x+y)y (Eq. a) \\
K_a=\frac{[H^+][A^-]}{[HA]} \\
Ka=\frac{(x+y).x}{C_{A0}-x} (Eq. b) \\
K_w=10^{-14} \\
K_a=1.8 \times 10^{-5} \\
C_{A0}=0.57 \times 10^{-9} \\
[/tex]
Solve (Eq. a) and (Eq. b) simultaneously in x and y to get
[tex]
x=5.6684 \times 10^{-10} \\
y=9.9717 \times 10^{-8} \\
[H^+] = x+y = 1.0028 \times 10^{-7} \\
[/tex]
By Borek's shortcut
[tex]
[H^+] = \sqrt{C_{A0} \times K_a} = 1.013 \times 10{-7} \\
[/tex]
QED?
Two wrongs make a right? The Kw effect compensates for neglecting the HA dissociation?
An analytical closed form solution might be more elegant though.....Still working on it.