Lines near the band origin in the high-resolution infrared spectrum of 12C16O are observed at 2131.58, 2135.50, 2139.38, 2147.04, 2150.81 and
2154.55 cm-1. Assign Jinitial and Jfinal quantum numbers to each transition
and, hence, determine the rotational constant of this molecule in both the v = 1 and the v = 0 vibrational levels. Determine the band origin.OK so, in the P branch:
2131.58 J=2
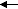
J=3
2135.50 J=1
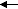
J=2
2139.38 J=0
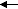
J=1
ΔE=hν
0+hB[J(J+1)-J'(J'+1)]
ΔE=hν
0+hB[J(J-1)-J(J+1)]
ΔE=hν
0-2hBJ
R branch:
2147.04 J=1
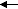
J=0
2150.81 J=2
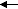
J=1
2154.55 J=3
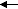
J=2
R branch: ΔE=hν
0+hB[J(J+1)−J′(J′+1)]
ΔE =hν
0 +hB [(J+1)(J+2)-J(J+1)]
ΔE =hν
0+2hB(J+1)
These are the equations I've found but I'm guessing that they're not right as I don't have v
0, but I can't do the rotational constant from the line spacing because they're all different? Just need a point in the right direction, not the answer, thanks.